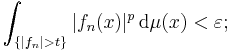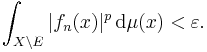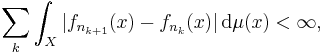Vitali convergence theorem

In mathematics, the Vitali convergence theorem is a generalization of the better-known dominated convergence theorem of Henri Lebesgue. It is useful when a dominating function cannot be found for the sequence of functions in question; when such a dominating function can be found, Lebesgue's theorem follows as a special case of Vitali's. The result is named after the Italian mathematician Giuseppe Vitali.

Statement of the theorem

Let (X, Σ, μ) be a measure space; let p ≥ 1 and let f_n : X → R belong to L^p(X, Σ, μ) for each natural number n ∈ N. Then f_n converges as n → ∞ to another measurable function f : X → R in L^p (i.e., in p^th mean) if and only if

f_n converges in measure to f;

the |f_n|^p are uniformly integrable in the sense that,

— for every ε > 0, there exists some t ≥ 0 such that, for all n ∈ N,

$\int_{ \{ | f_{n} | > t \} } | f_{n} (x) |^{p} \, \mathrm{d} \mu (x) < \varepsilon;$

— and, for every ε > 0, there exists some measurable set E ⊆ X with finite μ-measure such that, for all n ∈ N,

$\int_{X \setminus E} | f_{n} (x) |^{p} \, \mathrm{d} \mu (x) < \varepsilon.$

(If X has finite μ-measure, then this third condition is always satisfied, since one can take E = X in every case.)

Strategy of proof when p = 1

When p = 1, a subsequence can be found so that

$\sum_k \int_X |f_{n_{k%2B1}}(x) - f_{n_k}(x)| \, \mathrm{d}\mu(x) < \infty,$

which implies that the subsequence converges in L¹. The limit is necessarily equal to f. Arguing that this subsequence can be found as subsequence of any given subsequence shows that the whole sequence tends to f in L¹-norm.

References

Folland, Gerald B. (1999). Real analysis. Pure and Applied Mathematics (New York) (Second edition ed.). New York: John Wiley & Sons Inc.. pp. xvi+386. ISBN 0-471-31716-0. MR 1681462
Rosenthal, Jeffrey S. (2006). A first look at rigorous probability theory (Second edition ed.). Hackensack, NJ: World Scientific Publishing Co. Pte. Ltd.. pp. xvi+219. ISBN 978-981-270-371-2. MR 2279622

External links

Vitali convergence theorem at PlanetMath.